After the recent release of the Pwned Passwords v8 dataset, it was time to update my Bloom Filter implementation of Pwned Passwords!

Bloom Filters

If you aren't familiar with what a Bloom Filter is then you're going to find out how absolutely awesome they are. I have a detailed blog post that explains everything you need to know about Bloom Filters called Frequency analysis on hundreds of billions of reports at Report URI: Bloom Filters. If that isn't enough and you want to know even more, a Bloom Filter is a Probabilistic Data Structure and I have a whole selection of blog posts about them!

We use Probabilistic Data Structure a lot at Report URI but I did a demo of using a Bloom Filter to store and query the entire ~25 GB Pwned Passwords (v7) dataset with only ~2.7 GB of RAM, When Pwned Passwords Bloom! This blog post is the updated version for the latest release of Pwned Passwords, v8.

Updating to Pwned Password v8

Because of the nature of Bloom Filters, I could simply take the diff between the Pwned Password v7 and Pwned Passwords v8 data and add only the new passwords to the Bloom Filter. This would have an impact on the accuracy of the results though as it would affect the probability of a false positive (p) occurring. For the Pwned Password v7 Bloom Filter, I used the following values for filter creation:

m = 23,524,963,270 (2.74GiB)
n = 613,584,246 (passwords in v7)
k = 27 (hash functions)
p = 0.00000001 (1 in 99,857,412 false positive)

As you can't change the dimensions of a filter (m) after it has been created, the only choice you have would be to simply add the new items from v8 and take the hit on the probability of a false positive:

m = 23,524,963,270 (2.74GiB)
n = 847,223,402 (passwords in v8)
k = 27 (hash functions)
p = 0.00000268 (1 in 372,513 false positive)

As you can see, that's quite a significant increase in the probability of the filter giving us a false positive and that big hit is caused by the filter being overpopulated. There are 38% more password in v8 than in v7, the filter was simply never meant to hold this much data. You can see here the false positive probability calculations for the v7 and v8 filter and you can see exactly where the higher number of items in the filter is causing the problem. As the number of items in the filter (n) gets closer to the number of bits in the filters (m), the false positive probability increases rapidly.

p = pow(1 - exp(-k / (m / n)), k)
p = pow(1 - exp(-27 / (23,524,963,270  / 613,584,246)), 27)
p = 0.00000001

p = pow(1 - exp(-k / (m / n)), k)
p = pow(1 - exp(-27 / (23,524,963,270  / 847,223,402)), 27)
p = 0.00000268

To help visualise it better, here's a graph showing p against an increasing value of n where m = 23,524,963,270 and as you can see, there's clearly a point at which the false positive rate starts to climb.

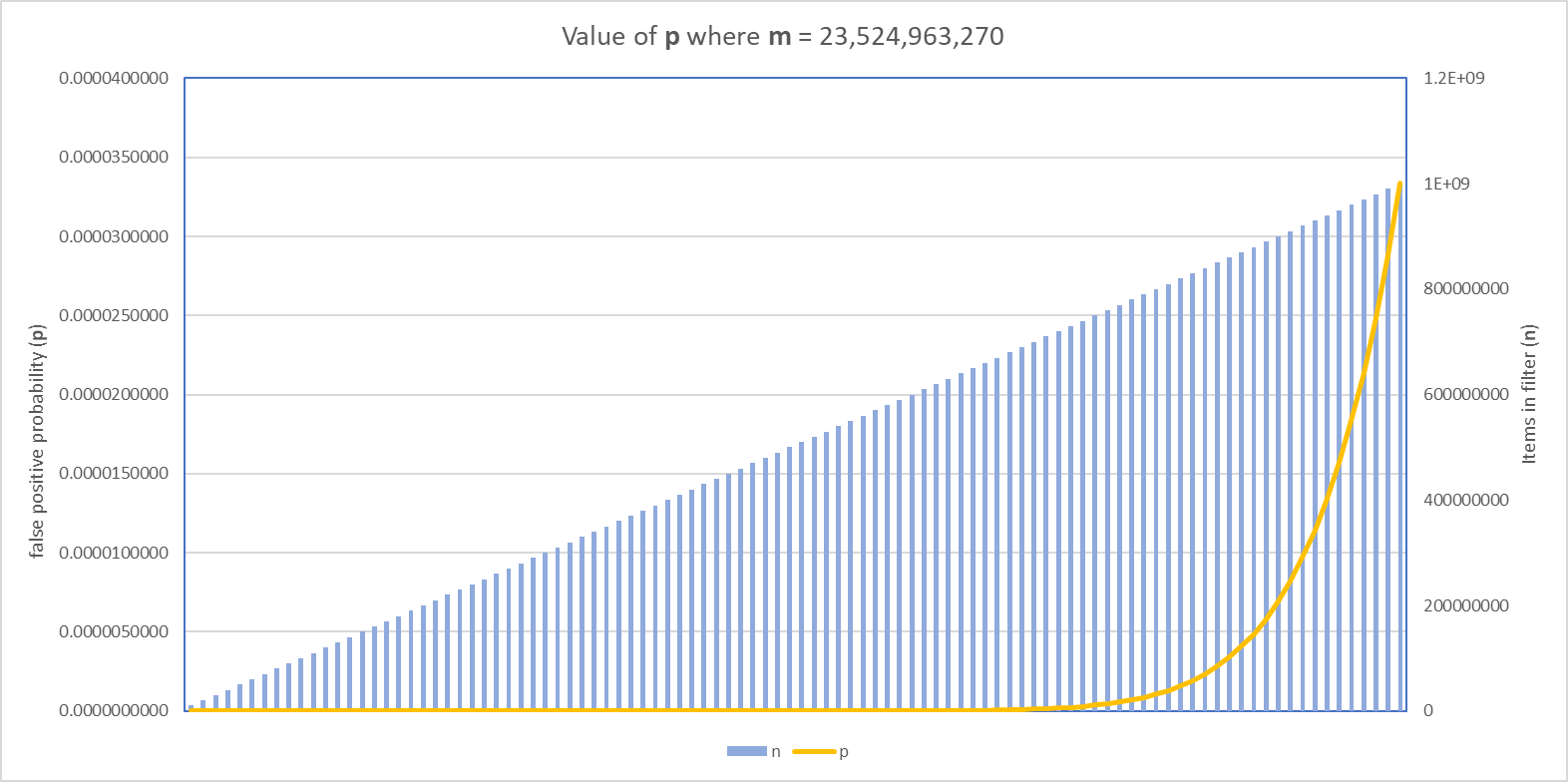
It turns out that the point at which we really start to hurt p is n = ~700,000,000 which is right around here.

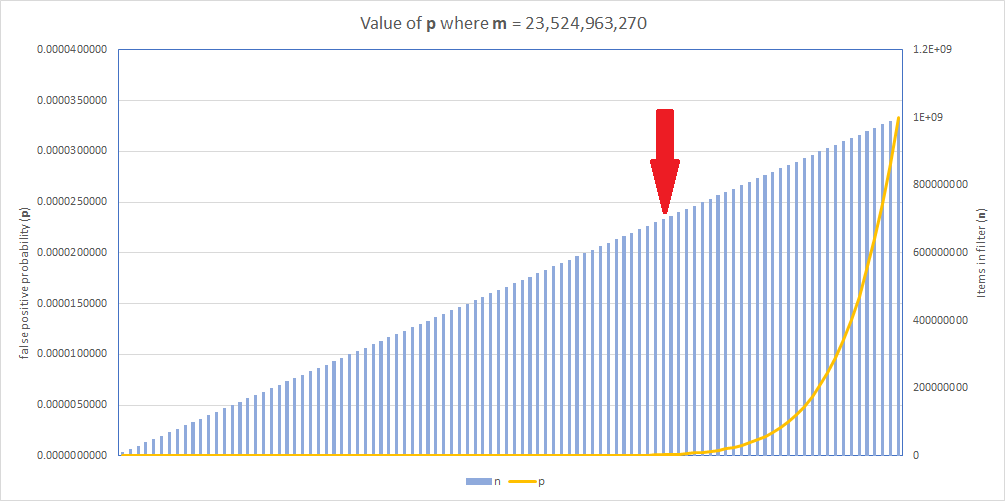
With a value of n = 847,223,402 for the new v8 data, we're well into the region where p is increasing quickly and this is why I'm re-generating the filter with new values.

Generating a new Bloom Filter

Given the significant change in the size of the dataset, the best thing to do is generate a new Bloom Filter for Pwned Passwords v8. To maintain the same probability of a false positive, we're going to have to increase the size of the filter.

m = 32,482,743,068 (3.78GiB)
n = 847,223,402 (passwords in v8)
k = 27 (hash functions)
p = 0.00000001 (1 in 99,857,412)

p = pow(1 - exp(-k / (m / n)), k)
p = pow(1 - exp(-27 / (32,482,743,068  / 847,223,402)), 27)
p = 0.00000001

When we look at the graph for the new filter, consider that the y-axis for p has changed significantly, but we are still achieving the same value for p.

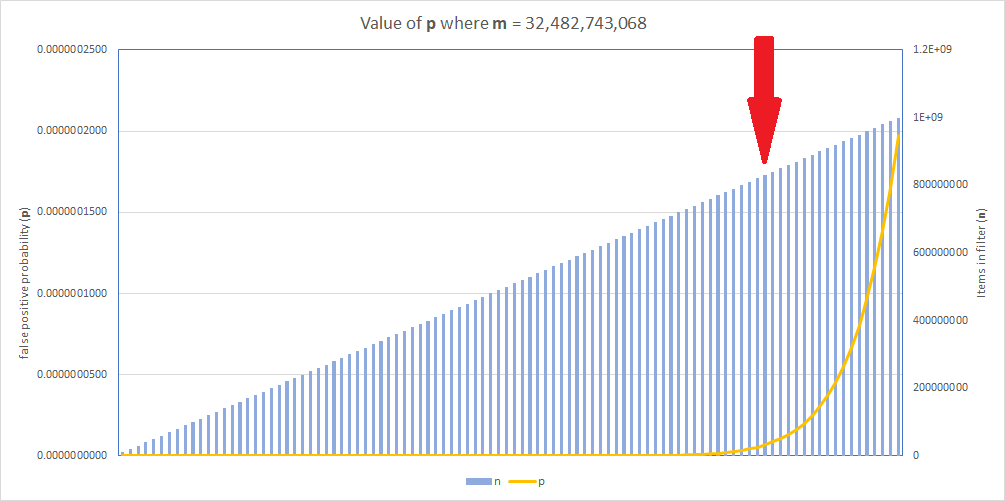
By increasing the size of the filter we can offset the impact of the increased number of items in the filter, but, the filter will need to increase in size from ~2.74 GB to ~3.78 GB. It's quite a large increase, but it's still an acceptably small amount of memory to use! It took ~17.5 hours to generate the filter.

...
FFFFFFF8A0382AA9C8D9536EFBA77F261815334D 847223400
FFFFFFFC219DCA98B2D9DE3C67D5714C5C51989E 847223401
FFFFFFFEE791CBAC0F6305CAF0CEE06BBE131160 847223402
Execution time: 1050.2261654496m

Testing it out!

As before, I did a basic set of queries against the filter to try it out.

password1234 pwned in 0.00032401084899902ms.
troyhuntsucks not pwned in 0.000075101852416992ms.
hunter1 pwned in 0.000068902969360352ms.
scotthelmerules not pwned in 0.000056028366088867ms.
chucknorris pwned in 0.000051975250244141ms.

As you can see, the filter is still blazing fast and actually, because of the changes I made, the performance of the filter isn't really going to change. Talking of performance, though, this tweet from Troy Hunt caught my eye...


I wondered just how fast the Bloom Filter could be so I grabbed the 100k passwords list from the NCSC and decided to run them against the filter! 

Checked 100,000 passwords in 3.320ms. That's 30,117,850 passwords per second!!
There were 99,934 pwned passwords and 66 passwords that were not pwned.

Yep, that's pretty fast! Of course, all 100k passwords here should be pwned but it turns out there were some problems with the data and not with my filter, the filter is 100% accurate. You can see more details in this thread.


As before, if you'd like to download the Pwned Passwords Bloom Filter, here is the raw dump file and a zipped version for your consumption!

dump.rdb
dump.zip